Hipérbola: definición, fórmula, elementos, ecuación, ejemplos,…

Aquí encontrarás todo sobre la hipérbola: qué es, cuáles son sus elementos característicos, cómo hallar su ecuación, ejemplos, ejercicios resueltos,…

¿Qué es una hipérbola?

La hipérbola es una curva abierta de dos ramas, cuya definición matemática es la siguiente:

En geometría analítica, una hipérbola es el lugar geométrico de los puntos del plano que cumplen la siguiente condición: el valor absoluto de la diferencia de las distancias desde un punto cualquiera de la hipérbola hasta dos puntos fijos (llamados focos) debe ser constante.

Además, el valor de la resta de esas dos distancias siempre es equivalente a la distancia entre los dos vértices de la hipérbola.

\lvert d_1 - d_2 \rvert = 2a

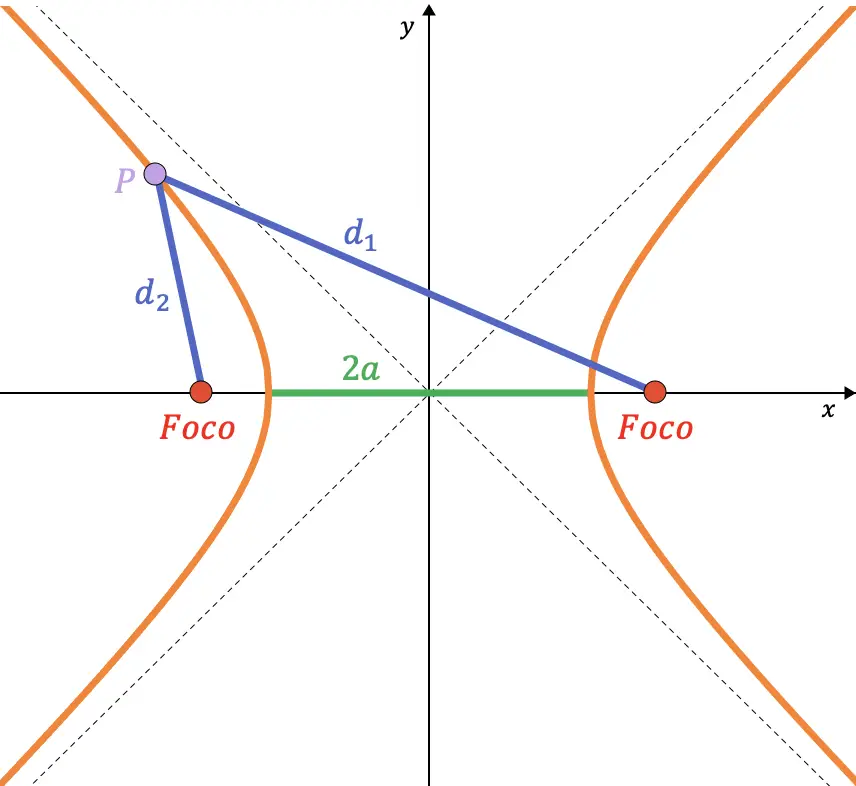
definicion de la hiperbola

Más abajo veremos qué significa el coeficiente a de una hipérbola.

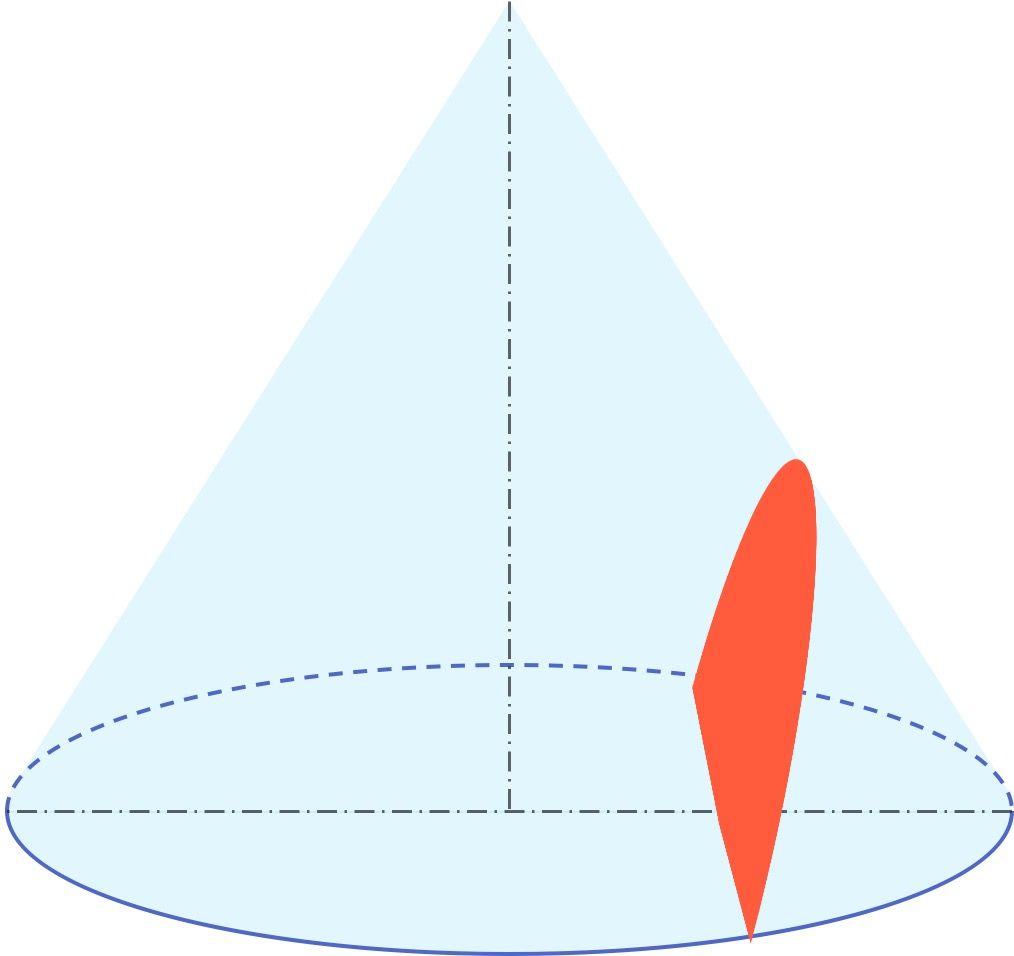
hiperbola seccion conica o conicas

Además, la hipérbola forma parte del grupo geométrico llamado cónicas junto a la circunferencia, la elipse y la parábola. Por lo tanto, una hipérbola se trata de una sección cónica, o dicho de otra forma, se puede obtener a partir de un cono.

En particular, una hipérbola es el resultado de cortar un cono mediante un plano con un ángulo menor que el ángulo que forma la generatriz del cono respecto a su eje de revolución.

Elementos de una hipérbola

Las características de una hipérbola dependen de los siguientes elementos:

  • Focos: son dos puntos fijos característicos de cada hipérbola (puntos F y F’ en el gráfico de abajo). El valor absoluto de la diferencia entre las distancias de cualquier punto de la hipérbola a cada foco es constante e igual a 2a.
  • Eje focal o principal: es la recta que pasa por los dos focos de la hipérbola. Corresponde a un eje de simetría de dicha figura geométrica. También se llama eje transverso o transversal.
  • Eje secundario: es la mediatriz del segmento FF’ (recta que pasa por los puntos B y B’). Además, es una recta perpendicular al eje focal y es otro eje de simetría de la hipérbola
  • Centro (O): es el punto de intersección de los dos ejes y el punto medio de los dos vértices y los dos focos. Como la hipérbola tiene dos ejes de simetría, también es el centro simétrico.
  • Vértices (A y A’): son los puntos donde se cortan las ramas de la hipérbola con el eje focal.
  • Radios vectores (R): son los segmentos que van desde cualquier punto de la hipérbola hasta cada foco.
  • Distancia focal: es la longitud del segmento compuesto entre los dos focos.
  • Eje mayor o real: es el segmento que va desde el punto A hasta el punto A’, su longitud es equivalente a 2a.
  • Eje menor o imaginario: es el segmento que va desde el punto B hasta el punto B’, su longitud es equivalente a 2b.
  • Asíntotas: son las rectas discontinuas representadas en la gráfica. Más abajo veremos cómo se calculan.
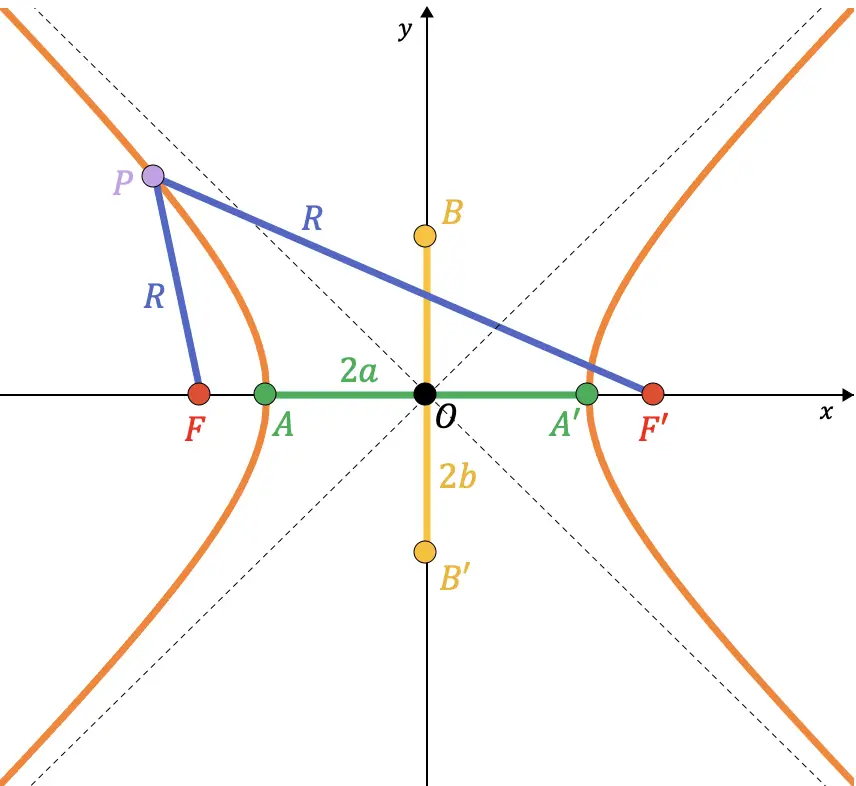
elementos de la hiperbola

Relación entre los elementos de una hipérbola

En primer lugar, se dice semieje a la mitad de un eje. Por ejemplo, el semieje real es el segmento que va desde el punto A hasta el centro de la hipérbola, cuya longitud es a.

Así pues, existe una relación muy importante entre el semieje real, el semieje imaginario y la semidistancia focal. De hecho, la fórmula que deduciremos a continuación se utiliza bastante para resolver ejercicios y problemas de hipérbolas.

Debes saber que los puntos B y B’ de una hipérbola corresponden a los puntos donde se cruzan el eje principal y la circunferencia imaginaria de radio c (semidistancia focal) con centro en el punto A. En consecuencia, como puedes ver en la siguiente representación gráfica, el segmento que une el punto A y el punto B coincide con el radio de dicha circunferencia (c):

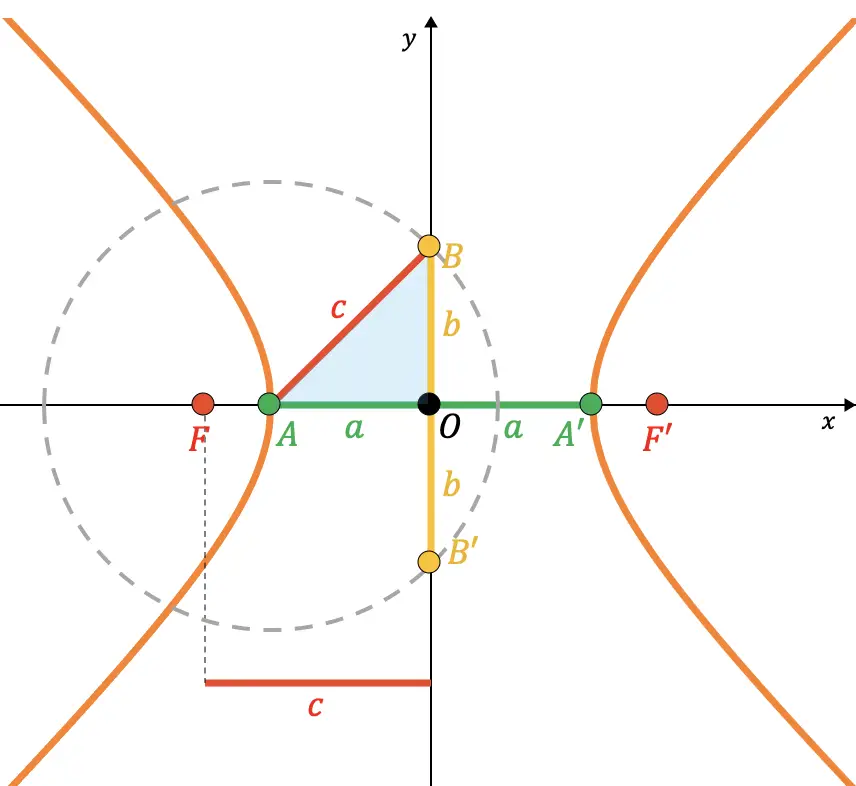
relacion entre los elementos de una hiperbola

De forma que se puede demostrar a partir del teorema de Pitágoras que la relación entre los parámetros a, b y c es la siguiente:

c^2 = a^2+b^2

Ecuación de la hipérbola

Existen varios tipos de ecuaciones de la hipérbola, ya que dependiendo de sus propiedades se usa una u otra para expresarla matemáticamente. A continuación vamos a analizar cada una detalladamente.

Primero de todo, tenemos la ecuación ordinaria de la hipérbola. En segundo lugar, veremos una variante de la ecuación ordinaria, se trata de la ecuación reducida o canónica de la hipérbola. Luego estudiaremos cómo es la ecuación general de una hipérbola. Y, por último, analizaremos las ecuaciones de dos casos particulares de hipérbolas: la hipérbola equilátera y las hipérbolas conjugadas.

Ecuación ordinaria de la hipérbola

Cuando queremos definir mediante una ecuación una hipérbola con centro fuera del origen de coordenadas (punto (0,0)), debemos usar la siguiente fórmula:

La fórmula de la ecuación ordinaria de la hipérbola en coordenadas cartesianas es la siguiente:

\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1

Donde:

  • x_0 y y_0 son las coordenadas del centro de la hipérbola: O(x_0,y_0)
  • a es la longitud del semieje mayor de la hipérbola.
  • b es la longitud del semieje menor de la hipérbola.

Con está ecuación se pueden describir hipérbolas cuyo eje focal es horizontal (ramas abiertas hacia la izquierda y hacia la derecha), que es como son las hipérbolas normalmente. Pero si estamos trabajando con un eje focal vertical (ramas abiertas hacia arriba y hacia abajo), el signo negativo cambia de la variable y a la variable x:

\cfrac{(y-y_0)^2}{a^2}-\cfrac{(x-x_0)^2}{b^2} = 1

Donde x_0 y y_0 son, igual que antes, las coordenadas del centro de la hipérbola y los términos a y b siguen siendo el semieje mayor y el semieje menor de la hipérbola, aunque, a diferencia de antes, estos dos ahora estarán orientados verticalmente y horizontalmente respectivamente.

Ecuación canónica o reducida de la hipérbola

Este tipo de ecuación de la hipérbola es muy parecida a la ecuación ordinaria, lo único distinto que tienen es que la ecuación canónica sirve para expresar analíticamente las hipérbolas cuyo centro es el punto (0,0). Por tanto, utilizamos la ecuación canónica o reducida de la hipérbola cuando el centro de la hipérbola es el origen de coordenadas.

Ahora procedemos a deducir la fórmula de la ecuación reducida de la hipérbola a partir de su ecuación ordinaria:

\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1

Si el centro de la hipérbola debe ser el origen de coordenadas, es decir el punto (0,0), siempre se cumplirá lo siguiente:

x_0 = 0

y_0 = 0

De modo que la fórmula de ecuación canónica o reducida de la hipérbola será:

\color{orange} \boxed{\color{black}\qquad\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1 \vphantom{\cfrac{\vphantom{\Bigl(}}{\vphantom{\Bigl(}}}\qquad }

Igual que antes, si el eje focal fuese vertical en vez de horizontal, la variable negada sería la x:

\cfrac{y^2}{a^2}-\cfrac{x^2}{b^2} = 1

Ecuación general de la hipérbola

La fórmula de la ecuación general de una hipérbola es la siguiente:

Ax^2 +Bxy+Cy^2 +Dx+Ey+F =0

Sin embargo, para que la ecuación anterior sea de una hipérbola, los coeficientes A y C deben ser diferente de cero y, a la vez, tener signo contrario.

Ecuación de la hipérbola equilátera

Una hipérbola equilátera es aquella en la cual la longitud del semieje real es equivalente a la longitud del semieje imaginario, esto significa que a=b. Por tanto, la ecuación de una hipérbola equilátera es de la siguiente forma:

\cfrac{x^2}{a^2}-\cfrac{y^2}{a^2} = 1

Además, la asíntotas de las hipérbolas equiláteras son perpendiculares entre sí. Y las ecuaciones de dichas rectas son las siguientes:

y=x

y=-x

Si nos fijamos bien, estas dos ecuaciones son las bisectrices del primer (y del tercer) cuadrante y del segundo (y cuarto) cuadrante respectivamente. De manera que si giramos 45º a la izquierda una hipérbola equilátera, sus asíntotas pasan a ocupar el lugar de los ejes de coordenadas:

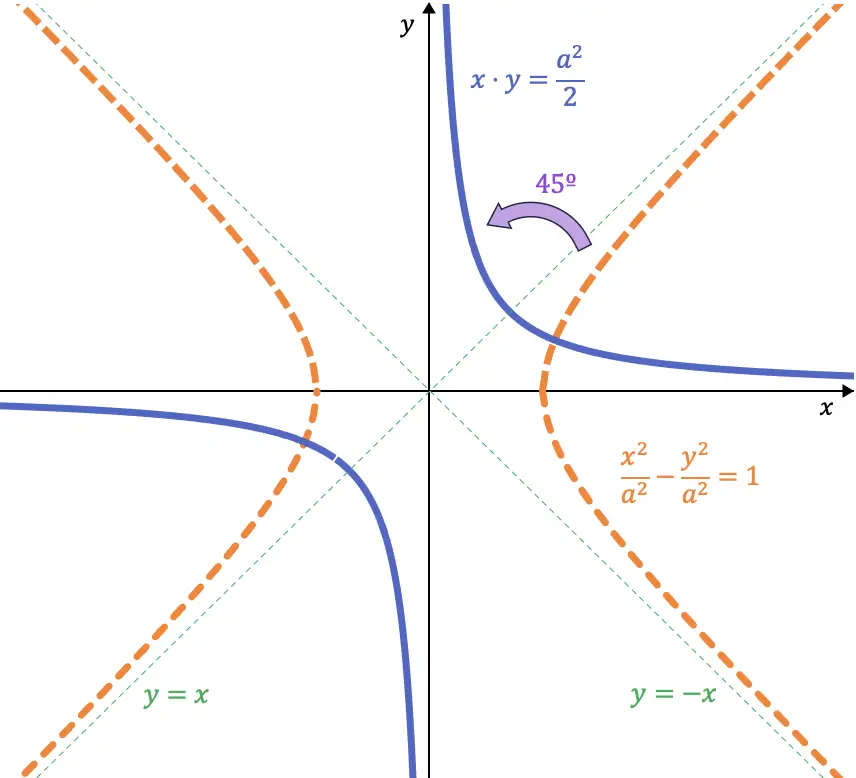
ecuacion de la hiperbola equilatera

Entonces, cuando hacemos el giro de 45º, la ecuación de la hipérbola queda de la siguiente forma:

x\cdot y = \cfrac{a^2}{k}

Hipérbolas conjugadas

Dos hipérbolas son conjugadas si el eje real de una de ellas es equivalente al eje imaginario de la otra. Por tanto, lo único diferente entre las ecuaciones de dos hipérbolas conjugadas es la variable que está negada, porque los coeficientes de los denominadores deben permanecer iguales.

A continuación tienes un ejemplo de las ecuaciones de dos hipérbolas que son conjugadas entre sí:

\cfrac{x^2}{a^2} - \cfrac{y^2}{b^2}=1 \qquad \qquad \cfrac{y^2}{b^2}-\cfrac{x^2}{a^2} =1

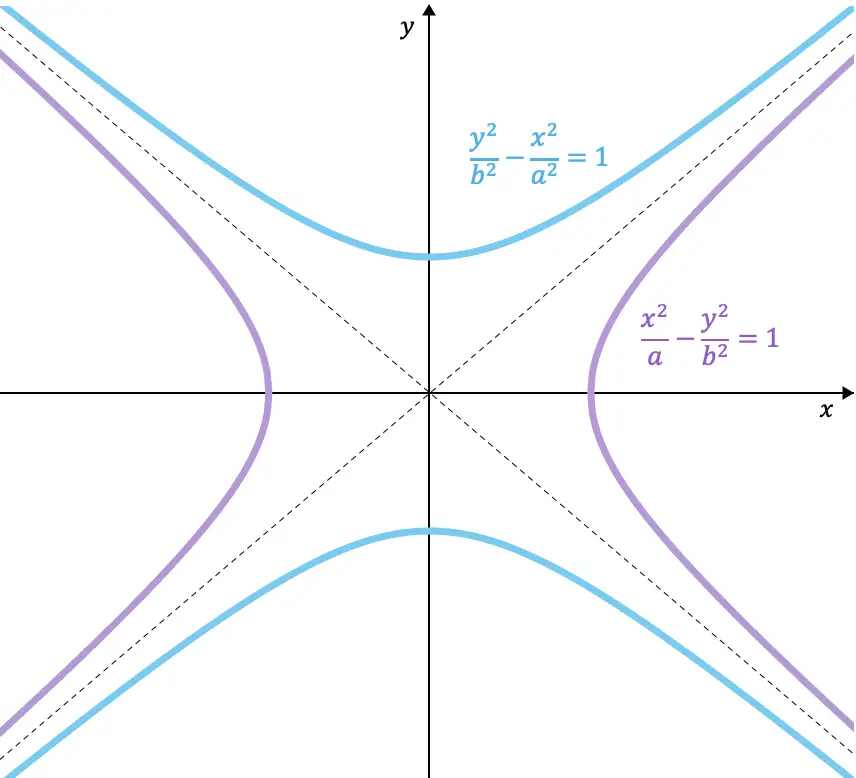
ecuaciones de hiperbolas conjugadas

Además, como puedes ver en las hipérbolas que se han representado gráficamente, las hipérbolas conjugadas comparten las mismas asíntotas.

Asíntotas de la hipérbola

Com has podido ver en los gráficos anteriores, toda hipérbola tiene dos asíntotas. Recuerda que una asíntota es una línea recta que se aproxima mucho a una función pero nunca llega a cruzarla ni a tocarla.

Entonces, las fórmulas que corresponden a las asíntotas de las hipérbolas son:

y= \cfrac{b}{a} x

y= -\cfrac{b}{a}x

De modo que las asíntotas de cualquier hipérbola se pueden determinar fácilmente a través de sus coeficientes a y b, que son las longitudes del semieje real y del semieje imaginario de la hipérbola respectivamente.

Excentricidad de la hipérbola

La excentricidad de una hipérbola es un parámetro característico que determina cuánto de abierta o cerrada es. Numéricamente, la excentricidad de una hipérbola se calcula dividiendo su semidistancia focal entre su semieje real:

e=\cfrac{c}{a}

La excentricidad de cualquier hipérbola siempre es más grande que 1:

e>1

El valor de este parámetro es bastante relevante, ya que nos indica la forma que tiene una hipérbola dada. Cuanto más cerca de 1 sea la excentricidad de una hipérbola más cerradas serán sus ramas, en cambio, cuanto mayor sea el valor de la excentricidad más abiertas serán sus ramas.

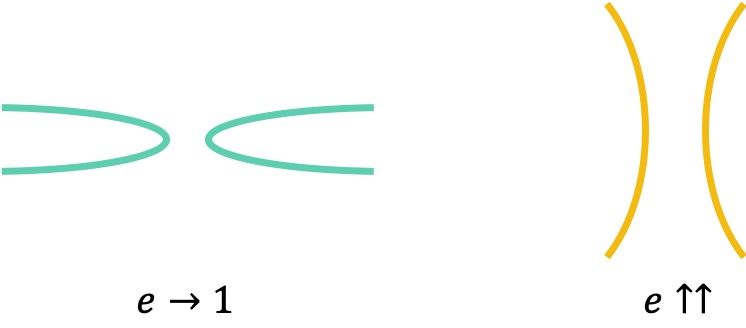
excentricidad de la hiperbola

Por último, cabe destacar que la excentricidad de una hipérbola equilátera siempre es igual a \sqrt{2}.

Ejercicios resueltos de hipérbolas

A continuación puedes practicar los conceptos que hemos visto con problemas y ejercicios resueltos de hipérbolas y de la ecuación de la hipérbola.

Ejercicio 1

¿Cuál es la ecuación de la hipérbola con centro en el punto (-1,3), una longitud del semieje real de 3 unidades y una longitud del semieje imaginario (paralelo al eje Y) de 7 unidades?

Para hallar la ecuación de la hipérbola simplemente tenemos que aplicar la fórmula de la ecuación ordinaria de la hipérbola:

\cfrac{(x-x_0)^2}{a^2}-\cfrac{(y-y_0)^2}{b^2} = 1

Sustituimos las coordenadas del centro de la hipérbola en la ecuación:

\cfrac{(x-(-1))^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1

\cfrac{(x+1)^2}{a^2}-\cfrac{(y-3)^2}{b^2} = 1

Y, finalmente, sustituimos los valores de las incógnitas a y b:

\cfrac{(x+1)^2}{3^2}-\cfrac{(y-3)^2}{7^2} = 1

\cfrac{\bm{(x+1)^2}}{\bm{9}}\bm{-}\cfrac{\bm{(y-3)^2}}{\bm{49}} \bm{= 1}

 

Ejercicio 2

Halla las coordenadas del centro, los vértices, los focos, el valor de la excentricidad y las asíntotas de la hipérbola cuya ecuación viene definida por:

\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1

Antes de nada, debemos notar que la variable negativa de la ecuación es la variable y, por lo que las ramas de la hipérbola se abrirán hacia la derecha y hacia la izquierda (eje focal paralelo al eje X).

En segundo lugar, la ecuación corresponde a la ecuación canónica (o reducida) de la hipérbola, así que su centro es el origen de coordendas.

\bm{O(0,0)}

Una vez sabemos el centro de la hipérbola, para calcular todo lo otro debemos encontrar el valor del semieje real (parámetro a) y del semieje imaginario (parámetro b). Ambos los podemos deducir a partir de la fórmula de la ecuación canónica (o reducida) de la hipérbola:

\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1

\cfrac{x^2}{25}-\cfrac{y^2}{144} = 1

a^2 = 25

a = \sqrt{25}

a = 5

b^2 = 144

b= \sqrt{144}

b = 12

De manera que si hay una distancia de 5 unidades entre el centro y los vértices, implica que los vértices de las hipérbolas son:

\bm{A(-5,0) \qquad A'(5,0)}

Para determinar las coordenadas de cada foco, debemos averiguar el valor de la semidistancia focal (parámetro c). Y, para ello, podemos usar la fórmula que relaciona los elementos de una hipérbola:

c^2 = a^2+b^2

c = \sqrt{a^2+b^2}

c = \sqrt{5^2+12^2} = \sqrt{169} =13

Por lo tanto, hay un espacio de 13 unidades entre el centro y los focos. Con lo que las coordenadas de cada foco son:

\bm{F(-13,0) \qquad F'(13,0)}

Luego, para calcular la excentricidad de la hipérbola debemos utilizar su fórmula correspondiente:

e= \cfrac{c}{a} = \cfrac{13}{5} = \bm{2,6}

Y, por último, hallamos las asíntotas de la hipérbola con sus fórmulas:

y= \cfrac{b}{a} x \ \longrightarrow \ \bm{y=}\mathbf{\cfrac{12}{5}}\bm{ x}

y= -\cfrac{b}{a}x \ \longrightarrow \ \bm{y=-}\mathbf{\cfrac{12}{5}}\bm{ x}

 

Ejercicio 3

Calcula la ecuación de la hipérbola con centro en el origen de coordenadas sabiendo que la diferencia de distancias desde un punto de la hipérbola hasta los focos F(-4,0) y F(4,0) es de 6 unidades.

Primero de todo, como la hipérbola tiene el centro en el origen de coordenadas, utilizaremos la ecuación canónica o reducida:

\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1

Luego, según la definición de hipérbola, el valor absoluto de la diferencia de distancias de cualquiera de sus puntos hasta los focos (que en este caso es 6) debe ser igual a la longitud del eje real (2a). Por tanto:

\lvert d_1 - d_2 \rvert = 2a

6 = 2a

\cfrac{6}{2} = a

3 = a

Por otro lado, el centro de la hipérbola es el punto (0,0) y un foco el punto (4,0). De modo que la distancia en ambos puntos (parámetro c) son 4 unidades.

c =4

Ahora podemos averiguar el valor del parámetro b con la relación matemática que hay entre los 3 coeficientes característicos de la hipérbola:

c^2 = a^2+b^2

b^2 = c^2-a^2

b = \sqrt{c^2-a^2}

b= \sqrt{4^2-3^2} = \sqrt{16-9} =\sqrt{7}

Así que la ecuación de la hipérbola es:

\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2} = 1

\cfrac{x^2}{3^2}-\cfrac{y^2}{\left(\sqrt{7}\right)^2} = 1

\cfrac{\bm{x^2}}{\bm{9}}-\cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Scroll al inicio