▷ Todas las Ecuaciones del Plano ✅ (fórmulas y ejemplos)

En esta página encontrarás cuáles son las fórmulas de todas las ecuaciones del plano y cómo se calculan. También hallarás cómo hallar la ecuación de cualquier plano con su vector normal. Además, podrás ver ejemplos y practicar con ejercicios resueltos de las ecuaciones del plano.

Índice

¿Qué es la ecuación del plano?

En geometría analítica, la ecuación de un plano es una ecuación que permite expresar matemáticamente cualquier plano. De modo que para hallar la ecuación de un plano solo se necesita un punto y dos vectores linealmente independientes que pertenezcan a dicho plano.

Antes de seguir con la explicación de las ecuaciones del plano es imprescindible que entiendas bien qué es el plano (geometría), ya que de lo contrario habrá cosas que no entenderás. Si no lo tienes del todo claro, puedes repasarlo en este enlace, donde hemos concentrado todo lo que debes saber sobre el plano.

¿Cuáles son las ecuaciones del plano?

Como hemos visto en la definición de la ecuación de un plano, se puede expresar cualquier punto de un plano plano como combinación lineal de 1 punto y 2 vectores.

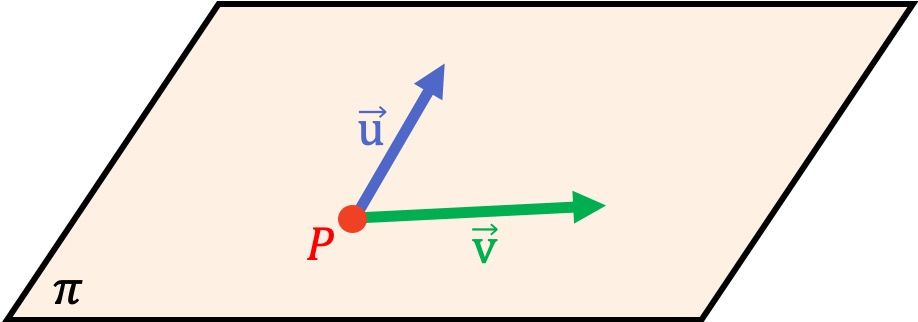
Sin embargo, una condición necesaria para que la ecuación corresponda a un plano es que los dos vectores del plano posean independencia lineal, o dicho con otras palabras, los dos vectores no pueden ser paralelos entre sí.

Así pues, todos los tipos de ecuaciones del plano son: la ecuación vectorial, las ecuaciones paramétricas, la ecuación implícita (o general) y la ecuación canónica (o segmentaria) del plano.

A continuación vamos a ver detalladamente la explicación y la fórmula de todas las ecuaciones del plano.

Ecuación vectorial del plano

Dados un punto y dos vectores directores de un plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La fórmula de la ecuación vectorial de un plano es:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

O, equivalentemente:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Donde $\lambda$ y $\mu$ son dos escalares, es decir, dos números reales.

Ecuaciones paramétricas del plano

La ecuación paramétrica de un plano se puede determinar a partir de su ecuación vectorial. A continuación puedes ver la demostración.

Sea la ecuación vectorial de un plano cualquiera:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Primero operamos y realizamos los productos de vectores por los escalares:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

Luego sumamos las componentes:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

Y, finalmente, conseguimos las ecuaciones paramétricas del plano igualando las coordenadas correspondientes a cada variable por separado:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Donde:

$\lambda$ y $\mu$ son dos escalares, es decir, dos números reales.
$\text{u}_x,\text{u}_y,\text{u}_z$ son las componentes de uno de los dos vectores directores del plano $\vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z).$
$\text{v}_x,\text{v}_y,\text{v}_z$ son las componentes del otro vector director del plano $\vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z).$

Ecuación implícita o general del plano

Dados un punto y dos vectores directores de un plano:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

La ecuación implícita, general o cartesiana de un plano se obtiene resolviendo el siguiente determinante e igualando el resultado a 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

De modo que la ecuación implícita o general del plano resultante será de la siguiente forma:

Este tipo de ecuación del plano también se llama ecuación cartesiana del plano.

Ecuación canónica o segmentaria del plano

La fórmula de la ecuación canónica o segmentaria de un plano es la siguiente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Donde:

$a$ es el punto de intersección entre el plano y el eje X.
$b$ es el punto de corte entre el plano y el eje Y.
$c$ es donde se cortan el plano con el eje Z.

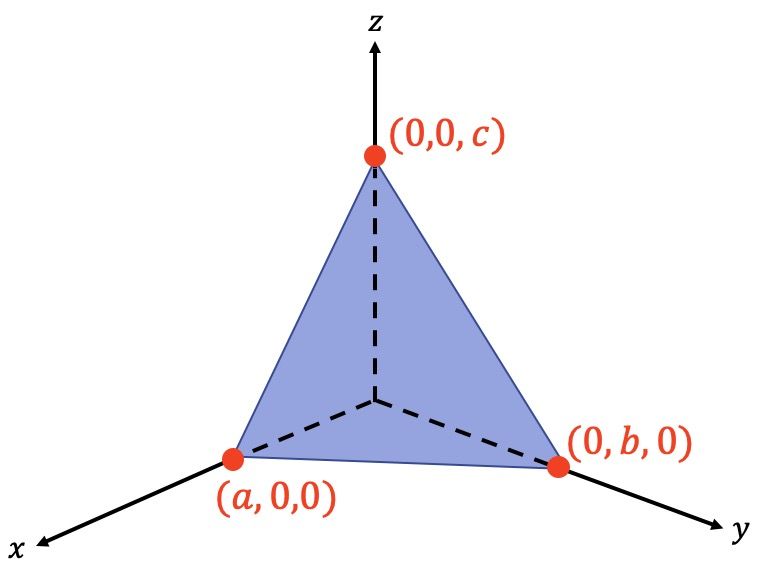
ecuacion segmentaria o canonica del plano bachillerato

La ecuación canónica (o ecuación segmentaria) del plano, también se puede obtener a partir de su ecuación general:

$Ax+By+Cz+D=0$

En primer lugar, despejamos el coeficiente D de la ecuación:

$Ax+By+Cz=-D$

Luego dividimos toda la ecuación del plano entre el valor del parámetro D cambiado de signo:

$\cfrac{Ax+By+Cz}{-D}=\cfrac{-D}{-D}$

$\cfrac{Ax}{-D}+\cfrac{By}{-D}+\cfrac{Cz}{-D}=1$

Y, mediante las propiedades de las fracciones, llegamos a la siguiente expresión:

$\cfrac{x}{-\frac{D}{A}}+\cfrac{y}{-\frac{D}{A}}+\cfrac{z}{-\frac{D}{A}}=1$

Por lo tanto, de esta expresión se deducen las fórmulas para calcular directamente los términos de la ecuación canónica o segmentaria de un plano:

$a=-\cfrac{D}{A} \qquad b=-\cfrac{D}{B} \qquad c=-\cfrac{D}{C}$

En consecuencia, para poder formar esta variante de las ecuaciones del plano es necesario que los coeficientes A, B y C sean diferentes de cero, evitando de esta manera las indeterminaciones de las fracciones.

Cómo calcular la ecuación de un plano a partir de su vector normal

Un problema muy típico de las ecuaciones de un plano es encontrar cómo es la ecuación de un determinado plano a partir de un punto y de su vector normal (o perpendicular). Así pues, veamos cómo se resuelve.

Pero primero debemos saber que las componentes X, Y, Z del vector normal a un plano coinciden respectivamente con los coeficientes A, B, C de la ecuación implícita (o general) de dicho plano.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Donde $\vv{n}$ es el vector ortogonal al plano $\pi.$

Una vez conocemos la relación anterior, veamos un ejemplo de cómo solucionar este tipo de problemas de ecuaciones del plano:

Determina la ecuación implícita o general del plano que pasa por el punto $P(1,0,-2)$ y uno de sus vectores normales es $\vv{n}=(3,-1,2) .$

La fórmula de la ecuación implícita, general o cartesiana de un plano es:

$Ax+By+Cz+D=0$

Entonces, a partir del vector normal, podemos averiguar los coeficientes A, B y C porque son equivalentes a las componentes de su vector normal:

$\vv{n}=(3,-1,2) \ \longrightarrow \ 3x-1y+2z+D=0$

De forma que solo nos queda hallar el parámetro D. Para ello, sustituimos las coordenadas del punto que pertenece al plano en la ecuación:

$P(1,0,-2)$

$3\cdot 1-0+2\cdot (-2)+D=0$

$3-4+D=0$

$-1+D=0$

$D=1$

De modo que la ecuación implícita o general del plano es:

$\bm{3x-y+2z+1 = 0}$

Ejercicios resueltos de la ecuación del plano

Ejercicio 1

Determina la ecuación vectorial del plano que contiene el vector $\vv{\text{u}}=(0,-2,3)$ y pasa por los siguientes dos puntos: $A(1,3,-1)$ y $B(2,-1,5).$

Ver solución

Para averiguar la ecuación de un plano se necesita un punto y dos vectores y en este caso solo tenemos un único vector, por lo que debemos hallar otro vector director del plano. Para ello, podemos calcular el vector que definen los dos puntos del plano:

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

Ahora ya sabemos dos vectores directores del plano y un punto, de modo que utilizamos la fórmula de la ecuación vectorial del plano:

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

Y sustituimos los dos vectores y cualquiera de los dos puntos del plano en la ecuación:

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

Ejercicio 2

Encuentra las ecuaciones paramétricas del plano que contiene los siguientes tres puntos:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

Ver solución

Para encontrar las ecuaciones paramétricas del plano, necesitamos hallar dos vectores linealmente independientes que pertenezcan al plano. Y, para ello, podemos calcular dos vectores que quedan definidos por los 3 puntos:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

Las coordenadas de los dos vectores hallados no son proporcionales, por lo que son linealmente independientes entre sí.

Ahora ya conocemos dos vectores directores y un punto del plano, de manera que aplicamos la fórmula de la ecuación paramétrica del plano:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Y sustituimos los dos vectores y cualquiera de los tres puntos del plano en la ecuación:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Ejercicio 3

Halla la ecuación implícita o general del plano que pasa por el punto $P(-2,1,3)$ y contiene los vectores $\vv{\text{u}}=(4,1,3)$ y $\vv{\text{v}}=(5,3,-1).$

Ver solución

Para calcular la ecuación de general o implícita del plano, debemos resolver el siguiente determinante formado por los dos vectores, las tres variables y las coordenadas del punto:

$\displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0$

Entonces, sustituimos los vectores y el punto en la fórmula:

$\displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0$

Y ahora resolvemos el determinante de la matriz 3×3 con el método que prefieras:

$12(z+1)+15(y-1)+1(x+2)-9(x+2)-4(y-1)-5(z+1) = 0$

Por último, hacemos las operaciones y agrupamos los términos similares:

$-8(x+2)+11(y-1)+7(z+1) = 0$

$-8x-16+11y-11+7z+7=0$

$-8x+11y+7z-20= 0$

Por lo que la ecuación implícita o general del plano es:

$\bm{-8x+11y+7z-20 = 0}$

Ejercicio 4

Determina si el punto $P(-1,5,-3)$ pertenece al siguiente plano:

$\pi : \ 2x+y+6z-5=0$

Ver solución

Para que el punto sea del plano, debe verificar su ecuación. Por tanto, tenemos que sustituir las coordenadas cartesianas del punto en la ecuación del plano y comprobar si se cumple la ecuación:

$2x+y+6z-5=0$

$P(-1,5,-3)$

$2\cdot (-1)+5+6\cdot (-3)-5=0$

$-2+5-18-5=0$

$-20\neq 0$

El punto no cumple con la ecuación del plano, por tanto, no forma parte de este plano.

Ejercicio 5

Averigua la ecuación segmentaria del plano cuya ecuación general (o implícita) es:

$3x-2y-6z+6=0$

Ver solución

Primero de todo, despejamos el término independiente de la ecuación:

$3x-2y-6z=-6$

Luego dividimos toda la ecuación del plano entre el valor del coeficiente D cambiado de signo:

$\cfrac{3x-2y-6z}{-6}=\cfrac{-6}{-6}$

$\cfrac{3x}{-6}+\cfrac{-2y}{-6}+\cfrac{-6z}{-6}=1$

Y, mediante las propiedades de las fracciones, llegamos a la siguiente expresión:

$\cfrac{x}{\frac{-6}{3}}+\cfrac{y}{\frac{-6}{-2}}+\cfrac{z}{\frac{-6}{-6}}=1$

Con lo que la ecuación segmentaria (o canónica} del plano es:

$\cfrac{\bm{x}}{\bm{-2}}+\cfrac{\bm{y}}{\bm{3}}+\cfrac{\bm{z}}{\bm{1}}=1$

Ejercicio 6

Calcula la ecuación implícita o general del plano en el espacio que pasa por el punto $P(3,4,-3)$ y uno de sus vectores normales es $\vv{n}=(5,-2,-3) .$

Ver solución

La fórmula de la ecuación implícita, general o cartesiana de un plano es:

$Ax+By+Cz+D=0$

Pues a partir del vector normal podemos averiguar los coeficientes A, B y C, ya que son iguales respectivamente a las componentes del vector normal:

$\vv{n}=(5,-2,-3) \ \longrightarrow \ 5x-2y-3z+D=0$

De forma que solamente nos falta averiguar el parámetro D. Para ello, sustituimos las coordenadas del punto que pertenece al plano en la ecuación:

$P(3,4,-3)$

$5\cdot 3-2\cdot 4-3\cdot (-3)+D=0$

$15-8+9+D=0$

$16+D=0$

$D=-16$

En conclusión, la ecuación implícita o general del plano es:

$\bm{5x-2y-3z-16 = 0}$

Ejercicio 7

Halla las ecuaciones paramétricas del plano que contiene la recta $r$ y es paralelo a la recta $s.$ Siendo las rectas:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

Ver solución

Para hallar las ecuaciones paramétricas del plano necesitamos conocer dos vectores directores y un punto de dicho plano. El enunciado nos dice que contiene la recta $r$ , por tanto, podemos coger el vector director y un punto de esa recta para definir el plano. Además, el enunciado nos dice que el plano es paralelo a la recta $s,$ por lo que también podemos utilizar el vector director de esa recta para la ecuación del plano.

La recta $r$ está expresada en forma de ecuaciones paramétricas, así que las componentes de su vector director son los coeficientes de los términos con el parámetro $t:$

$\vv{r} =(1,-3,2)$

Y las coordenadas cartesianas de un punto de esa misma recta son los términos independientes de las ecuaciones paramétricas:

$P(1,2,4)$

Por otra parte, la recta $s$ está en forma de ecuación continua, de manera que las componentes de su vector director son los denominadores de las fracciones:

$\vv{s} =(2,2,-3)$

Por tanto, las ecuaciones paramétricas del plano son:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Ecuaciones del plano en el espacio

¿Qué es la ecuación del plano?

¿Cuáles son las ecuaciones del plano?

Ecuación vectorial del plano

Ecuaciones paramétricas del plano

Ecuación implícita o general del plano

Ecuación canónica o segmentaria del plano

Cómo calcular la ecuación de un plano a partir de su vector normal

Ejercicios resueltos de la ecuación del plano

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

Ejercicio 7

Deja un comentario Cancelar respuesta