¡Bienvenid@ a geometriaanalitica.info!
En esta web encontrarás la explicación de todo lo relacionado con la geometría analítica: vectores, rectas, planos, distancias, ángulos, etc. Hemos incluido en cada tema ejemplos y ejercicios resueltos paso a paso, para que así puedas ver cómo se hace y puedas practicar. ¡Si aún así te queda alguna duda no dudes en escribirla en los comentarios de la página! ¡Te responderemos encantados! Solo tenemos un objetivo: ¡que consigas la mejor nota de la clase! 💪😘

Índice
¿Qué es la geometría analítica?
La definición matemática de geometría analítica es la siguiente:
La geometría analítica es la rama de las matemáticas que estudia las figuras geométricas mediante técnicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.
Es decir, la geometría analítica se encarga de analizar matemáticamente las distancias, los ángulos de inclinación, las áreas, los volúmenes, etc. de los diferentes elementos geométricos que existen.
Por ejemplo, cuando queremos calcular la distancia que hay entre dos puntos o el ángulo que forman una recta y un plano necesitamos utilizar las fórmulas de la geometría analítica.
Aunque más abajo profundizaremos más sobre estos conceptos, debes saber que a parte de la geometría analítica existen otros tipos de geometría: geometría algebraica, geometría plana, geometría del espacio, geometría descriptiva, geometría proyectiva, geometría euclidiana,…
Finalmente, la geometría analítica consiste en dos cuestiones fundamentales:
- Obtener la ecuación del lugar geométrico de un conjunto de puntos en un sistema de coordenadas.
- Dada la ecuación de un lugar geométrico en un sistema de coordenadas, determinar la representación gráfica de los puntos que verifican dicha ecuación.
Sistemas de coordenadas
Para poder emplear la geometría analítica es necesario un sistema de coordenadas, que es un sistema que nos permite identificar la posición de un punto, un vector, una recta, un plano,… en definitiva, cualquier objeto geométrico.
Al principio, cuando se empieza a estudiar la geometría analítica, se suele usar el sistema de coordenadas del plano cartesiano. Eso es debido a que se trata de un sistema de coordenadas bidimensional (2D) y, por tanto, es una manera de simplificar el estudio. Dicho sistema está formado por dos ejes de coordenadas: el eje X y el eje Y.
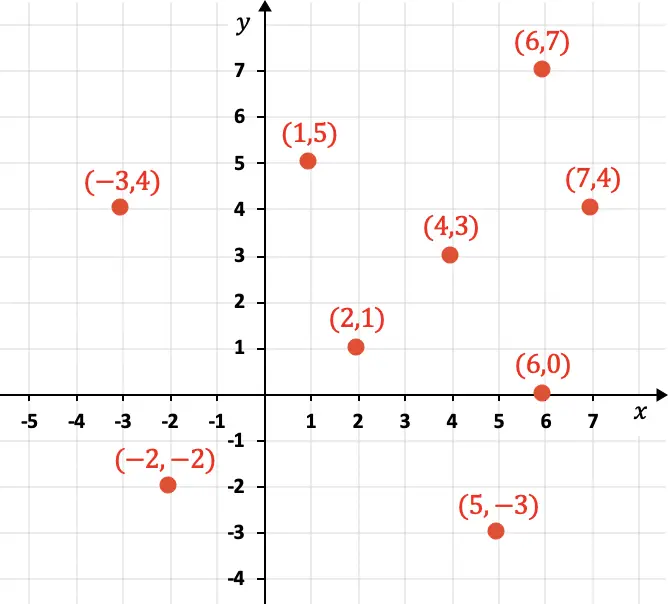
Sin embargo, los elementos geométricos están formados por 3 dimensiones (anchura, altura y profundidad), así que realmente se necesita un sistema de coordenadas tridimensional (3D) para poder analizarlos completamente.
Para distinguir estas dos variantes de la geometría analítica, se suele decir geometría analítica en el plano (o en R2) cuando operamos en dos dimensiones, y geometría analítica en el espacio (o en R3) cuando operamos en tres dimensiones.
Si estás más interesad@, aquí puedes ver la explicación detallada del sistema de coordenadas, donde, además, encontrarás otros tipos de sistemas de coordenadas bastante peculiares.
¿Cuál es la importancia de la geometría analítica?
La geometría analítica es muy importante en las matemáticas, ya que permite expresar analíticamente las figuras geométricas. Por lo tanto, mediante la geometría analítica se puede establecer una correspondencia entre elementos geométricos y ecuaciones algebraicas.
Esta propiedad da mucha importancia a la geometría analítica, porque gracias a ella se pueden reformular problemas geométricos en problemas equivalentes en álgebra (y viceversa) y, de esta forma, se pueden resolver dichos problemas científicamente.
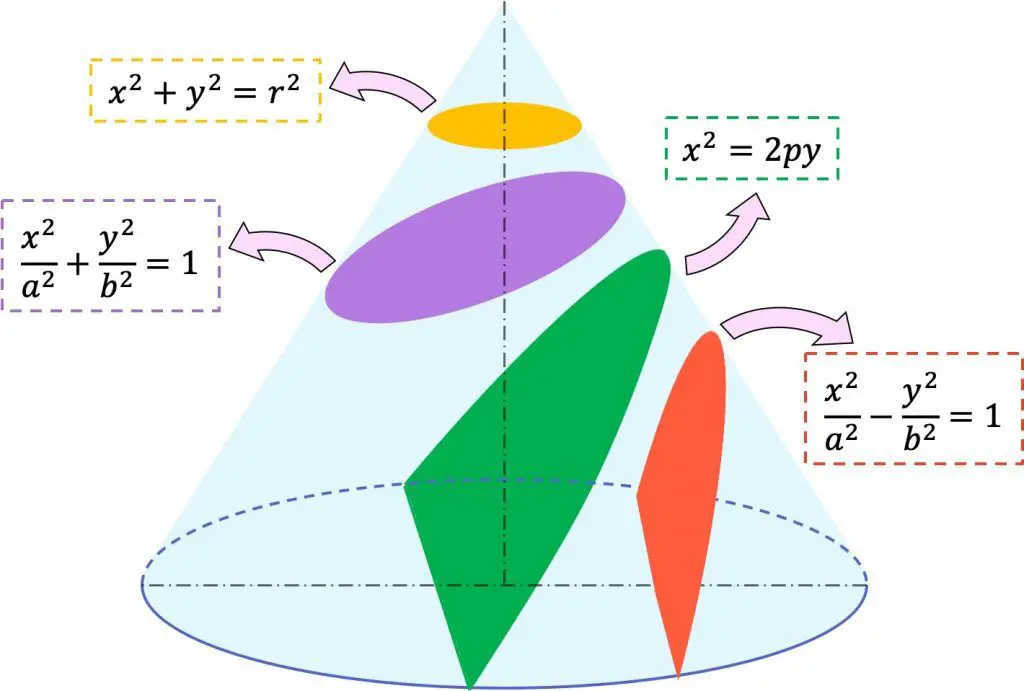
Como puedes ver en las figuras geométricas representadas arriba, se pueden transformar curvas geométricas en ecuaciones matemáticas gracias a la geometría analítica. En este caso particular, estas curvas (circunferencia, elipse, parábola e hipérbola) pertenecen a un grupo geométrico llamado secciones cónicas; puedes saber más sobre ellas en el enlace de más arriba (al principio de la página).
Por otro lado, la geometría analítica también es muy relevante debido a sus casi infinitas aplicaciones. Como veremos más abajo, la geometría analítica se utiliza muy frecuentemente en la vida real, especialmente en la ciencia, la ingeniería y la industria.
Finalmente, hay que tener en cuenta que la geometría analítica también es fundamental a nivel escolar. La geometría analítica se empieza a estudiar normalmente en secundaria en 4º de ESO (España) y se profundiza más en la materia en 1º y 2º de Bachillerato, ya que se suelen preguntar ejercicios de geometría analítica en la Selectividad (EBAU o EvAU).
Aplicaciones de la geometría analítica
Una vez hemos visto el significado de geometría analítica, veamos ahora para qué sirve esta rama de las matemáticas y de la física.
Seguramente, el uso más habitual de la geometría analítica es en los mapas. Cuando queremos saber nuestra localización en un mapa estamos utilizando sin querer las nociones de la geometría analítica. También, cuando un GPS encuentra la ubicación de un lugar o de un objeto está usando un sistema de coordenadas y, por tanto, la geometría analítica.
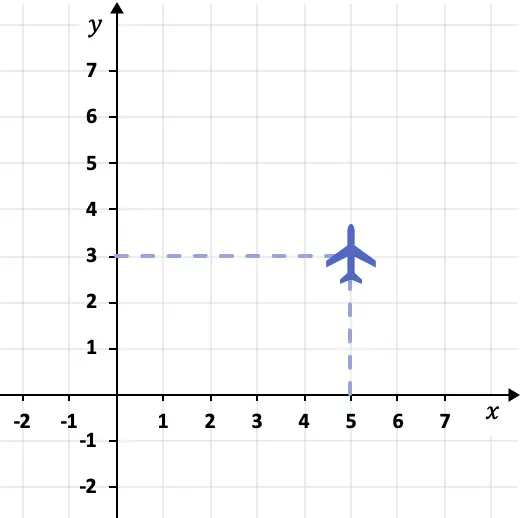
Evidentemente, los conocimientos de geometría analítica también se emplean en la arquitectura y en la construcción de edificios, como por ejemplo los puentes colgantes. Asimismo, la geometría analítica se usa mucho en la industria para fabricar antenas parabólicas, herramientas, automóviles, etc.
Actualmente, además de utilizarse para el cálculo matemático, la geometría analítica es fundamental en la animación de videojuegos o películas. Por ejemplo, se emplea para dar forma a seres animados mediante curvas geométricas.
Finalmente, otra utilidad de la geometría analítica es la observación geométrica. Gracias a esta ciencia se descubrió que las órbitas que describen los cuerpos celestes son elipses (Johannes Kepler) y no circunferencias, permitiendo así una mejor aproximación matemática de las trayectorias de los planetas.
Historia de la geometría analítica
Aunque evidentemente algunas propiedades geométricas ya se conocían anteriormente, se atribuye el inicio de la geometría analítica al matemático francés René Descartes con el apéndice La Geometría que se incluía en la publicación en el año 1637 de una de sus obras más conocidas: el Discurso del método. Por esta razón se suele llamar a la geometría analítica como geometría cartesiana.
Sin embargo, el geómetra Pierre de Fermat también participó activamente en el desarrollo y la promulgación de la geometría analítica durante el siglo XVII y, de hecho, probablemente él y Descartes fueron igual de importantes en la época. Pero se considera que Descartes fue el origen de este tipo de geometría porque su obra fue publicada antes (la obra Fermat es póstuma) y, además, los matemáticos posteriores a ambos se basaron principalmente en la obra de Descartes.
Por otro lado, cabe destacar que tanto Fermat como Descartes se fundamentaron en el trabajo realizado en la antigua Grecia por los matemáticos Diofanto, Euclides, Apolonio y Pappus, entre otros.
Durante el siglo XVII, el matemático Frans van Schooten, Florimond de Beaune y Johan de Witt contribuyeron a la explicación y a la divulgación de las ideas de Descartes. Fue durante ese periodo cuando la geometría analítica tuvo su máximo esplendor.
Así pues, la principal aportación de Descartes a la geometría analítica fue la creación de un sistema de coordenadas (por eso a veces se dice sistema de coordenadas cartesiano), de esta manera podía describir la posición de cualquier punto con un par de números y, a partir de aquí, realizar estudios.
El sistema de coordenadas cartesiano seguro que te resulta familiar, se trata de dos ejes perpendiculares: uno horizontal y otro vertical. El eje horizontal recibe el nombre de eje X (eje de abscisas) y el eje vertical se denomina eje Y (eje de ordenadas). Y ambos juntos son los famosos ejes de coordenadas cartesianos. Por otra parte, el hecho de que hoy en día aún se utilice y se enseñe este método para graficar puntos es la demostración de lo importante que fue este descubrimiento.
Otro logro significativo de Descartes dentro de la geometría analítica es el de definir una curva en el plano mediante una propiedad geométrica determinada, es decir, que una relación matemática sea suficiente para describir todos los puntos que forman parte de una curva. Esto permitió representar figuras geométricas mediante fórmulas matemáticas del tipo f(x,y)=0, utilizando sobre todo funciones polinómicas de primer y de segundo grado.
Esta propiedad deriva en las conocidas secciones cónicas. Con el avance de Descartes se pudo hallar las ecuaciones que definen la circunferencia, la elipse, la parábola y la hipérbola. Puedes saber más al respecto en el enlace de más arriba (al principio de la página), donde encontrarás qué son las cónicas, sus características, cómo se calculan sus ecuaciones, ejemplos, ejercicios resueltos paso a paso y mucho más.
En definitiva, los desarrollos de Descartes y Fermat darían la posibilidad de vincular los cálculos aritméticos con las operaciones geométricas y, en un nivel mayor de abstracción, cómo se vinculan las ecuaciones algebraicas de dos variables con determinadas curvas geométricas. Contribuyendo así a completar la geometría clásica y a plantear y resolver nuevos problemas geométricos.
En ese sentido, tal y como hemos visto en los ejemplos de lo que aportaron Descartes y Fermat a la geometría analítica, ambos basaron prácticamente todo su estudio en la geometría analítica plana, esto es, de 2 dimensiones. Pero, aunque ya sugirieron utilizar 3 coordenadas para poder analizar curvas y superficies en el espacio, la geometría analítica tridimensional no se acabó de desarrollar hasta mediados del siglo XVIII. Aquí destacan las figuras de los matemáticos Euler, Hermman y Clairaut, quienes averiguaron las ecuaciones generales para cilindros, conos y otras superficies de revolución.
Finalmente, fue en la segunda mitad del siglo XVIII con Leonhard Euler, Joseph-Louis Lagrange y Gaspard Monge, cuando se empezó a considerar la geometría analítica como una rama independiente de la geometría sintética (la geometría pura o no analítica).
Y, para terminar, después de la geometría analítica se empezó a desarrollar la geometría diferencial de Guass y ya más adelante, a principios del siglo XX, tuvo lugar la geometría algebraica.
